ファンクションジェネレータのFY6900をいじっているときに、VCOに興味を持ちました。自作のこぎり波発生回路のランプ波を自作VCOに入力して、電圧による周波数可変を実現したいと思いますが、その手始めにVCO回路を勉強し、電圧による周波数変化を実験してみます。
加える電圧で発振周波数を制御する発振器を”電圧制御発振器(VCO)”と呼びます。VCOはVoltage Controlled Oscillatorの略です。
回路の発振する周波数を変化させるには、共振器を構成するコイルかコンデンサの値を変えます。加える電圧によって電極間の容量が変わる”バリキャップダイオード”を使って発振周波数を変える方法がAM/FMラジオで使われているらしいです。
マクニカ VCO の概要
1S2638 Datasheet
シュミットトリガー74HC74版
ケース１
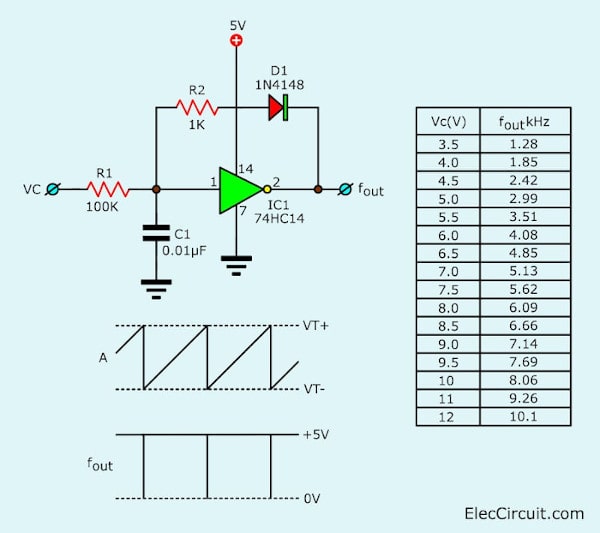
Simple vco using schmitt trigger using 74HC14
This is Simple VCO circuit using schmitt trigger using 74HC14__Hex inverting, which inside have 6 schmitt trigger, but applied one frequency controller
|
| Simple VCO using schmitt trigger using 74HC14 |
- チャージ時：74HC14のスレッショルド $V_{T+}$ まで、電流 $i=V_C/R_1$ でコンデンサ$C_1$ にチャージする。
- ディスチャージ時：74HC14のスレッショルド $V_{T-}$ に瞬間的に下がるので、それを補填すべくコンデンサ$C_1$ から$R_2, \,D_1$を通して放電される。
下記にLTspiceの時刻歴波形とVCO特性（制御電圧$V_f$ と発振周波数の関係）を示します。$V_f=4[V]$ です。
$V_f=4[V]$ での理論値周期613μsに対して、599μs (1.67kHz) でした。VCO周波数は引用元の値よりも少し低いようです。
ケース２
バリキャップを使ったアナログシンセ用VCO回路 (1)
バリキャップ（可変容量ダイオード）を使ってシンプルな楽器用のVCOができたので、回路や注意点などをまとめておきます。
 |
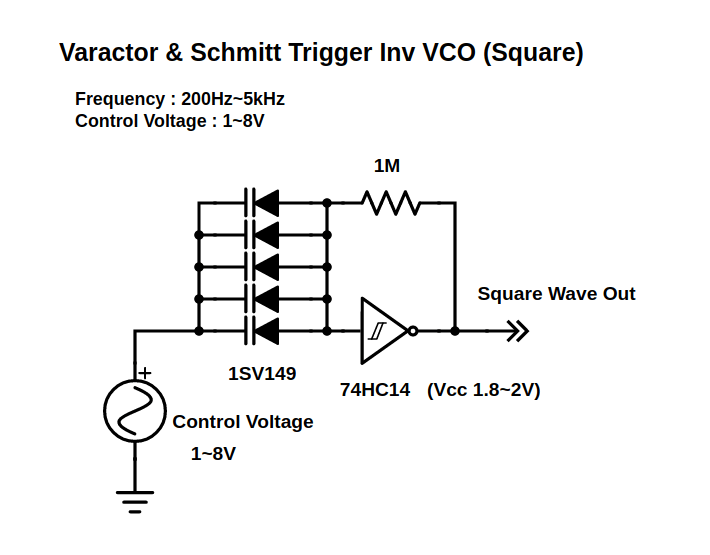| バリキャップを使ったアナログシンセ用VCO回路 (1) |
この回路の原理は理解できていません。バリキャップの特性は電圧を上げるとキャパシタ容量が減るので、発振周波数が上がるという仕組みだと思います。
このあとで実験しようと思っているので、手持ちのFM用バリキャップ（1s2638）と同等容量のFM1043を使って、固定キャパシタ回路との比較をシミュレーションします。
下図の左が固定容量キャパシタ回路を使う普通の74HC14発振回路で、右が当該ケースのバリキャップ式の発振回路です。
CとRは同じ設定でシミュレーションしてみた結果が下記です。似かよった周波数なのですが、バリキャップ回路がやや低い値になっています。L→Hのチャージ工程はほぼ同じ時間ですが、H→Lのディスチャージ工程で時間がかかっているのが原因のようです。順方向電流に働く抵抗成分があるような特性です。
動作の概要が分かったので、この回路のシミュレーションをします。チャージ時間はケース１の式(1)と同じです。電源電圧3V以上で有効です。
ディスチャージ時間は$V_T+$ から$V_T-$ への放電なので、次式で与えられます。チャージ時間よりも長くなります。ただし、これは上図左の固定容量キャパシタ回路でのディスチャージ時間なので、バリキャップ回路ではこれよりも長くかかるようです。
\[ \Delta t_D = C_1 R_1 \cdot ln \left ( \cfrac{V_{T+}}{V_{T-}} \right ) \tag2 \]
下記にLTspiceでシミュレーションした時刻歴波形と右にVCO特性（制御電圧$V_f$ と発振周波数の関係）を示します。$V_f=3[V]$ です。
$V_f=3[V]$ での(1)式チャージ時間43μsに対して、シミュレーションは53μsでした。また、(2)式ディスチャージ時間58μsに対して、シミュレーションは94μsでした。周期は147μs でVCO周波数は6.8kHzです。
ケース３
VCO的なのをサクッと作ってみる
久々にアナログ回路です。最近発振回路に興味を持ち始めまして、その興味の1つに VCO(Voltage Cont…
チャージ時間は先例とほぼ同じなのですが、ディスチャージ時間が随分長くなっています。これはR4が影響しており、この値を大きくするとディスチャージ時間が減少します。
引例の仕様（R2:100k ）ではVCO周波数が100kHzを超えたものになります。可聴域にするため下図の仕様に変更しました。
下記にLTspiceでシミュレーションした時刻歴波形と右にVCO特性（制御電圧$V_f$ と発振周波数の関係）を示します。$V_f=0[V]$ です。
この回路の特徴は前の2事例と違いバリキャプ設定電源を74HC14のH/L動作と分離できることです。そのため電圧0VからがVCOの制御電圧にできます。シミュレーション仕様では6～13kHzの周波数変更が可能です。
シミュレーションまとめ
実験
ケース１
組付けた素子の値は表のとおりです。
この条件で実験した結果をシミュレーションと比較すると図のようになりました。同じ制御電圧に対して、実験値はシミュレーションの2倍ほどの発振周波数になっています。9.5Vを超えたあたりから、12kHzが10kHzに急減する現象が出ました。
今回の実験は電圧で周波数が変わることを確認することが目的なので、急減の現象や値のシミュレーションとの不一致は気にしないことにします。
シミュレーションどおりに入力側電圧はランプ波形となり、出力側電圧はHigh側のスレッショルドで瞬断/放電され0Vになる波形が観察できました。
$V_f=3, 10V$ 間での可変倍率は、$\cfrac{10.6}{1.46}=7.3$倍 でした。水色波形に表れているH/Lスレッショルド間のヒス幅は、両条件ともに0.8V程度です。
 |
| $V_f=3V$ |
 |
| $V_f=10V$ |
ケース３
組付けた素子の値は表のとおりです。バリキャップは1s2638を使いました。このspice modelはないので、シミュレーションでは類似特性と思われるFV1043です。
バリキャップの電圧に対する特性を下図に示します。測定は5個並列の値を測り、1/5にしています。
この条件で実験した結果をシミュレーションと比較すると下図のようになりました。制御電圧に対して、実験の方が発振周波数が2倍くらい大きく、電圧に対する周波数の変化量も2倍くらい大きい結果となりました。
今回の実験は電圧で周波数が変わることを確認することが目的なので、値のシミュレーションとの不一致は気にしないことにします。
$V_f=0, 5V$ の2ケースでのオシロ波形を載せます。紫：$V_f$(オシロDC)、水色：74HC14 入力側電圧(オシロAC)、黄色：74HC14出力側電圧(オシロDC)です。
制御電圧で発振周波数が変化する特性が確認できました。ただし、次のシミュレーションとは異なる現象があります。
入力側電圧波形では上下のスレッシュルドで電圧が飛ぶような現象が出ています。また、シミュレーションではディスチャージ時間が長い現象だったのですが、チャージ、ディスチャージがほぼ同じ割合でした。
$V_f=0, 5V$ 間での可変倍率は、$\cfrac{20.4}{10.2}=2$倍 でした。水色波形に表れているH/Lスレッショルド間のヒス幅は、工程単独で見ると両条件ともに0.8V程度ですが、工程の切換りで飛んでいます。
 |
| $V_f=0V$ |
 |
| $V_f=5V$ |
実験結果
- ケース１では8倍弱（3V, 1.46kHz から 10V, 10.6kHz ）
- ケース２では2倍（0V, 10.2kHz から 10V, 20.4kHz）
