homeHome / create_new_folder発振器 /

のこぎり波発振回路

published_with_changes 更新日： event_note 公開日：

labelLTspice label発振器

のこぎり波を作る方法は色々あるようです。基本的な考え方はオペアンプを使った積分回路です。周波数の変更を可変抵抗や積分コンデンサの選択で調整するので、設計も使い勝手も結構大変そうに思います。

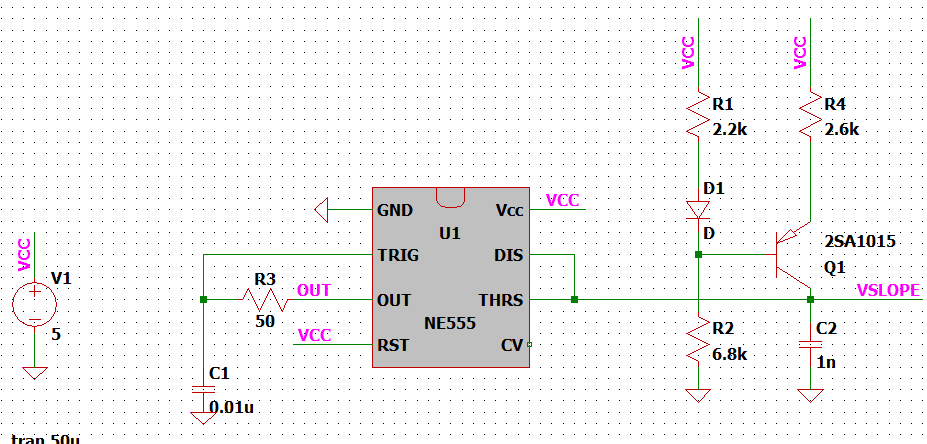
色々調べていると、次のYoutube動画を見つけました。周波数、ゲイン、オフセットを独自に変更できる回路で、555 ICとオペアンプでの構成されています。説明も明確で回路図も添付されています。試しにこれを作ってみることにしました。

のこぎり波発生の仕組み

のこぎり波は555 ICとそこにぶら下がる定電流回路が積分コンデンサC2を充放電することで得られます。555 ICのスレッショルド間（1/3･VCCから2/3･VCC）で充放電が起こります。電流一定でコンデンサを充電するので、電圧は直線的に上昇してランプ状（のこぎり波）になります。詳しくは次のブログに載っています。

「タイマIC LM555を使ったのこぎり波発生回路」

ねがてぃぶろぐ　NE555でのこぎり波

タイマICとして有名なNE555の応用回路のほとんどは、CRの時定数を利用した発振回路です。
CRの時定数を用いる方法は、電源電圧に依存せずCとRの値だけで周波数を決定できる利点があります

gomisai.blog75.fc2.com
SLOPE回路(ノコギリ波形発振回路)をタイマIC NE555とPNPトランジスタ2SA1015を使ってLTspiceでシミュレーションをする

SLOPE回路(ノコギリ波形発振回路)をタイマIC NE555とPNPトランジスタ2SA1015を使ってLTspiceでシミュレーションをする

どうも。本日はSLOPE回路をLTspiceでシミュレーションした結果を報告します。手に入れやすいNE555と2SA1015で作成しました。SLOPE回路は一定周波数でノコギリ状の波形で発振を続ける回路のことです。DCDCコンバータではPW

kakitamablog.com


回路図の動作を理解するためにLTspiceでシミュレーションします。オペアンプはLM358を両電源で使います。実際にブレッドボードに組む時もLM358を使いました。（LM358は回路図の推奨オペアンプです。）

のこぎり波\sawtooth7.asc

周期（理論値）

のこぎり波形（回路図のsign）の周期を求めてみます。カレントミラー回路で得られる定電流が積分コンデンサをチャージするので、その過程を上記の回路図に示す記号を使って表します。

チャージ電流 $i$ は、
\[i=\cfrac{VCC-V_E}{R_E} \tag{1}\]
で表せます。ここで、$V_E$はエミッター・ベース電位$V_{BE}$と抵抗分圧されたバイアス電圧を使って、
\[ V_E=V_{BE}+\cfrac{R3}{R2+R3} \cdot VCC \tag{2}\]
このように表せます。

一方、積分コンデンサC2は定電流 $i$ によってチャージされます。その関係を電荷$Q$と容量$C$のコンデンサのチャージ電圧$V_C$を使って表すと次になります。$t$ は時間です。
\[Q=C \cdot V_C=i\cdot t\] 
この関係より、時刻 $t$ におけるコンデンサ電圧は次式で表せませす。
\[V_C=\cfrac{1}{C}\cdot i \cdot t \tag{3}\]
$C$ と $i$ が一定の条件のもとで、コンデンサ電圧 $\cfrac{1}{3}VCC$ から $\cfrac{2}{3}VCC$ までのチャージするときの電位差を$\Delta V_C$、 チャージ時間を$\Delta t$ として式(3)を積分すると、
\[\Delta V_C=\cfrac{1}{C} \int_{t1}^{t2} i dt =\cfrac{i}{C} [t2-t1]=\cfrac{i}{C}\Delta t\]
チャージ時間に比べ放電時間は非常に小さいので無視すると、$\Delta t$ がのこぎり波の周期になります。
\[ \Delta t = \cfrac{C}{i} \Delta V_C \tag{4} \]
$\Delta V_C$ は時刻 $t1$における電圧 $\cfrac{1}{3}VCC$ から $t2$における電圧 $\cfrac{2}{3}VCC$ までの電位差 $\cfrac{1}{3}VCC$ なので、
\[ \Delta t = \cfrac{C}{i} \cdot \cfrac{1}{3}VCC \]
この式の $i$ を式(1) で表して、$V_E$ に式(2)を代入して整理すると、周期は下記の式で表せます。
\[\Delta t = \cfrac{1}{3} \cdot \cfrac{VCC \cdot C \cdot R_E \, (R_2+R_3)}{R_2 \cdot VCC - V_{BE}(R_2+R_3)} \tag5\]
$R_2$ は抵抗分圧するときのVCC側の抵抗であることに注意が必要です。

シミュレーション結果

基本設定

$C\,:\,0.22\mu F, \;R_E\,:\, 2.97k\Omega$ でのシミュレーション結果です。時間の経過とともにコンデンサ電圧 V(sign) が上昇し、$\cfrac{2}{3}VCC$になるとトリガ Lとなって、V(sign)は放電で急峻に$\cfrac{1}{3}VCC$ に落ちた後、再度チャージを繰り返す動作がシミュレーションできました。
周期は理論値852μsに対して、918μsであり, 勾配(slope)は理論値 3.0/$918^{-6}$=3270 [V/A] に対して、3410[V/A]でした。

式(5)に示すように、周期は電源電圧VCCに依存しますが、ポテンシオで$R_E$を変えることにより単独で変更が可能になります。


Amplitude（増幅度）変更

基本設定の7Vp-p振幅に対して、ポテンシオを10%変えると約1Vほど振幅を増減できます。



Off Set変更

基本設定に対して、オフセット用のポテンシオを10%変えると、だいたい2Vほどオフセットを変更できます。

電源電圧が9Vなので、LM358の動作電圧の関係からマイナス1.5Vの7.5Vで頭打ちとなっています。


ブレッドボード回路で実験

ブレッドボード回路

写真の回路を組み特性評価を行いました。


実験：こぎり波の出力とVCO

下記は周波数1kHz, 振幅5Vp-p, オフセット 0Vに調整した時の波形を示します。トリガ Lが1msごと（1kHz）に繰り返され、その間にのこぎり波が発生しています。放電するトリガ Lの時間は実測で6μsですが、シミュレーションでは1μsでした。

上から4番目の青色波形は、この回路で出力される紫色ののこぎり波（Saw）を使って、VCO（電圧制御発振器）を試してみたものです。Saw波形をFY6900のVCO-INに入力して、Saw波形の0～5Vのリニアな変化に対して、発振器が1kHzから50kHzにスイープするように設定しました。狙い通り、周波数のスイープが観察できました。




下の例は、VCO出力を振幅スイープとしたケースです。これも狙い通りに動作させることができました。


実験：周波数レンジ

コンデンサC2の容量を変えると、設定できる周波数レンジを変更できるので試してみました。

オペアンプがLM358では15kHzが限界のようです。これは”振幅が縮小しない”という基準で見たものです。波形の乱れは10Hzを超えたあたりの、もう少し低い周波数から発生します。

そこで、オペアンプをLT1364に替えたところ、100kHzまできれいな波形を得られるようになりました。一方、低周波側ではLT1364は3Hzを下回ると発信しなくなるのに比べ、LM358では1Hzまで安定した発振が可能でした。


発振周波数
C2コンデンサLM358LT1364
[μF]min. [Hz]max. [Hz]min. [Hz]max. [Hz]
1001.5416.4314.3
0.227578.06k7578.2k
0.11.2k12.5k1.2k12.8k
0.0110k15k(ability limit)9k96k
1nーー61.7k260k

代表的なケースでの実験波形を載せておきます。

LM358での発振波形

LM358 c2:100uF 1.54Hz （発振する下限周波数）

LM358 c2:0.22uF 1.54Hz （きれいな発振波形の下限周波数）

LM358 c2:0.01uF(10nF) 10kHz （これより高周波数では波形乱れがひどい）

ここからはLT1364での発振波形

LT1364 c2:100uF 3Hz （これより低い周波数では発振しない）

LT1364 c2:0.1uF 10kHz 

LT1364 c2:0.001uF(1nF) 100kHz （これより高周波数では波形乱れがひどい）

LT1364 c2:0.001uF(1nF) 260kHz （調整範囲の上限周波数）

実験：シュミットトリガ74HC14で自作VCO

先に載せたVCO実験はFunction Generatorの FY9600を使ったものですが、簡易的なVCOを74HC14とバリキャップで自作してみました。このVCOは単独で実験してみると、０～5Vに対して100～250kHzの矩形波が得られます。

Saw波形の上昇と共に矩形波の周波数が増えることを予想していたのですが、なぜか周波数は約170kHzで変わらずデューティが変わっているようです。原因究明は今のところはやらないことにします。

自作 VCO


まとめ

  • 今回使用したのはバイポーラ版の555 ICです。積分コンデンサC2に使った0.001μFはデータシートに示された下限の容量です。$R_E$の値をいじったり、CMOS版の555と高速なオペアンプを使えばもっと高周波数まで作れるかもしれませんが、それは今後の課題です。
  • 今回の実験ではLT1364で100kHzが波形も含めた上限でした。LM358では10kHzが上限でした。
  • 低周波数側では、LM358と積分コンデンサに100μFの組み合わせで、周波数1Hz程度を得ることができました。100μFはデータシートの上限値です。$R_E$が10kΩだと、1Hz程度の低い周波数では発振しないようです。
  • 発振が得意な555 ICなので、参考動画と同様の設定では苦労することなく発振させることができました。
  • 自分で作った発振回路でVCOにすることができ、ちょっと感激しました。
  • FY6900と比べたら、桁違いに見劣りする性能ですが、ものづくりを十分理解楽しめます。より低周波、より高周波への拡張へと期待が膨らみます。

Powered by Blogger | Designed by QooQ

keyboard_double_arrow_down

keyboard_double_arrow_down